Background
Classical computers operate using bits, representing 0 or 1. While powerful, it faces challenges for specific computational problems. In addition to that, classical computing, driven by Moore’s Law, faces a bottleneck as chips approach the atomic scale, encountering disruptive quantum phenomena.

In 1981, Paul Benioff proposed the concept of a quantum Turing machine, the quantum analogue of the classical Turing machine, which is computing device that manipulates symbols on a strip of tape according to a set of rules, designed to model the logic of any computer algorithm. This laid the groundwork for the development of quantum computers.


In the same year, Richard Feynman, a prominent American physicist, highlighted the inefficiency of classical computers in simulating quantum systems. He proposed the utilization quantum systems for simulating other quantum systems. The following is a famous quote by him:
Nature isn’t classical, dammit, and if you want to make a simulation of nature, you’d better make it quantum mechanical, and by golly it’s a wonderful problem, because it doesn’t look so easy.

After that, David Deutsch conceptualized the universal quantum computer in 1985 and established its equivalence to the classical counterpart. His theoretical framework paved the way for quantum algorithms advancements.

Nine years later, Peter Shor demonstrated the capability of quantum computers to factorize large numbers exponentially faster than the best-known classical algorithms. This implies the possibility of breaking the widely used Rivest-Shamir-Adleman (RSA) encryption scheme.

Quantum Bits (Qubits)
A quantum bit (qubit) is the fundamental unit of quantum information, capable of existing in multiple states simultaneously (superposition). Entanglement, another unique property, allows qubits to be correlated in ways not possible in classical systems.

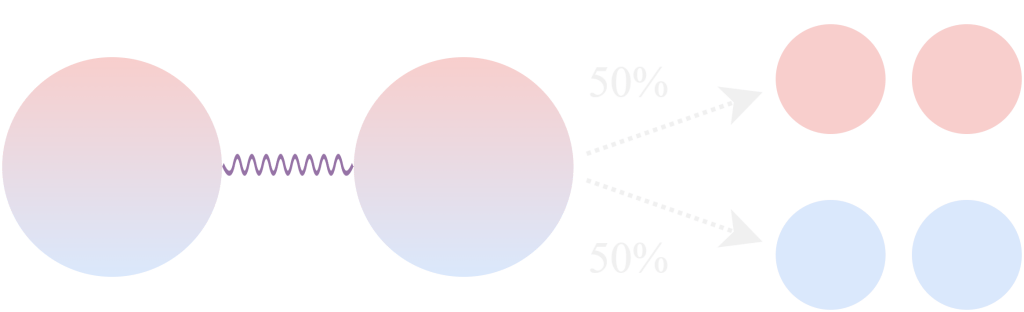
A qubit exists in a superposition state of both logical bits:
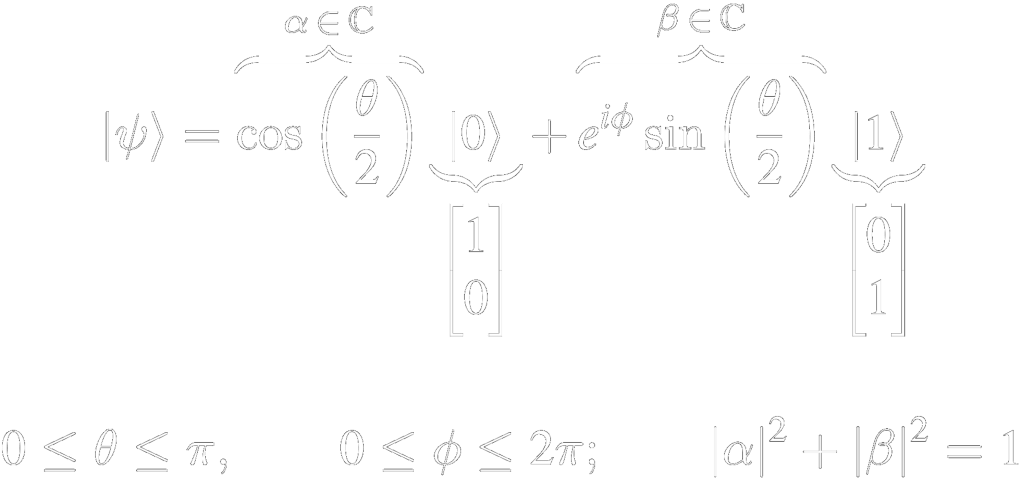
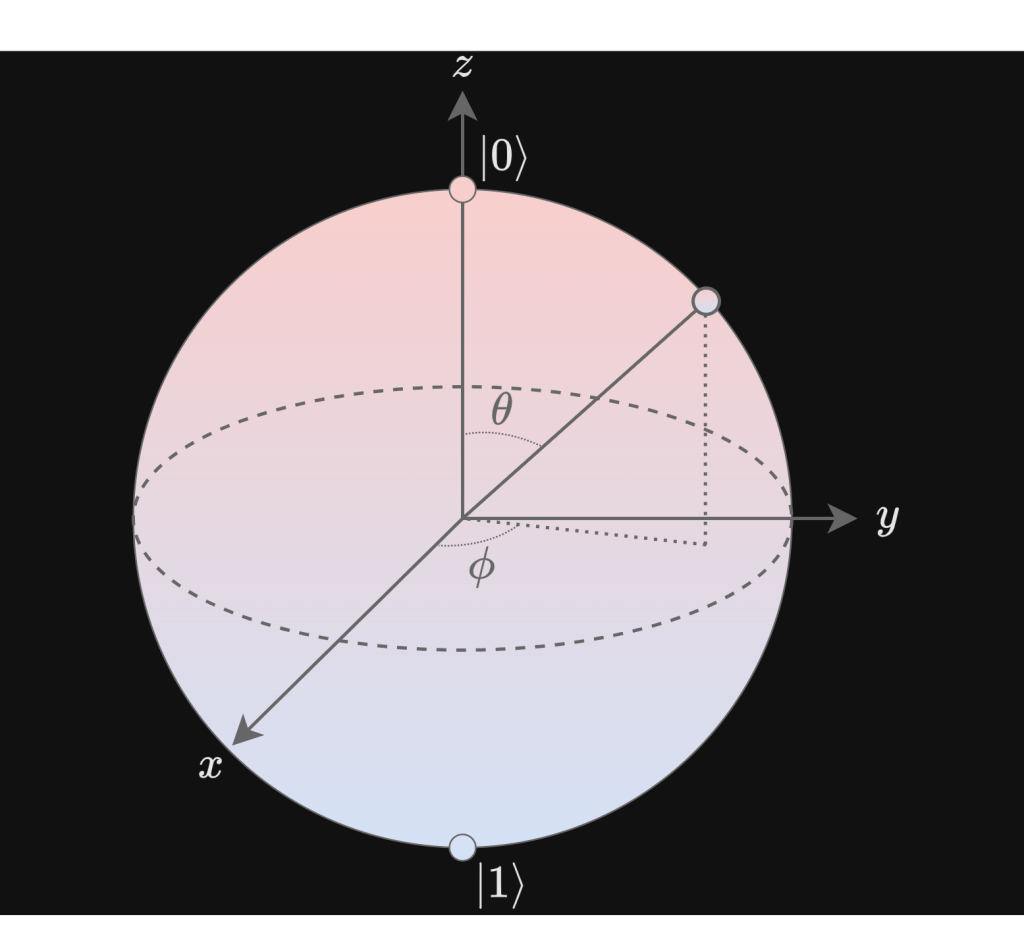
where the magnitude represents the qubit’s probability of being in one logical state. Geometrically, a qubit can be depicted using the Bloch sphere.
Quantum Advantage
Qubits enable quantum parallelism, allowing simultaneous probing of possibilities.

| Time Efficiency | Resource Efficiency | |
| Serial Computing | Low | High |
| Parallel Computing | High | Low |
| Quantum Computing | High | High |
Quantum algorithms offer significant speedup for some computational problems.
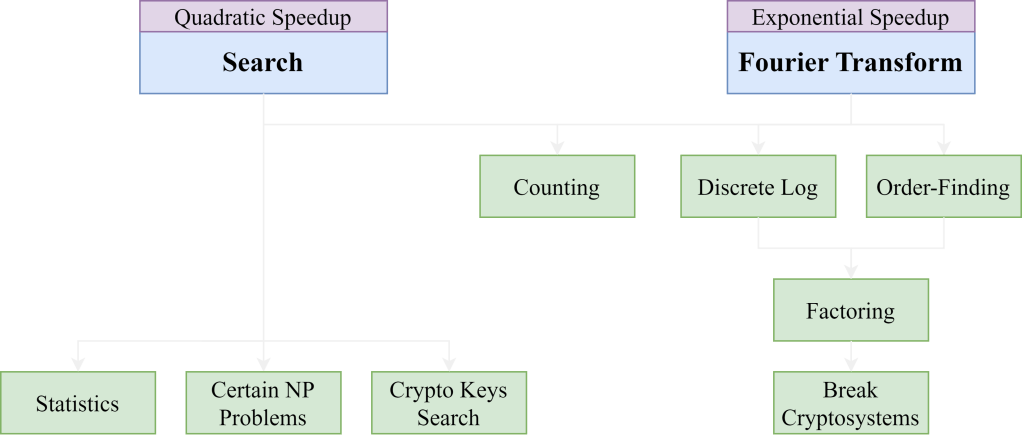
Specifically, the obtained complexity reductions for notable algorithms are tabulated below.

Unlike classical computing, which is intuitive for our human brains, quantum mechanics is bizarre. This makes it much harder to develop novel quantum algorithms that operate faster than the best-known classical counterparts.
